Principal

Disinfection Contact Time and Kinetics

by Eric Karch and David Loftis

Introduction

Brief History

Factors That Affect Contact Time

Applications to Real Systems

Credits and Links

Introduction

Water is disinfected but never completely sterilized in the water treatment process. This disinfection is a two part process that includes:

Removal of particulate matter by filtration. A rule of thumb is that high turbidity in the effluent is a potential health risk, because viruses and bacteria can hide within the rough texture of particulates. Therefore, removal of the particulates reduces the chance of pathogenic microorganisms in the effluent. (Refer to Figure 1)
Inactivation of pathogenic microrganisms by chlorine, chlorine dioxide, ozone, or other disinfectants

Contact time and kinetics are simply a measure of the inactivation due to time and concentration of the disinfectant. The USEPA has developed regulations for the minimum kill percentages (inactivation) necessary for public water to be considered potable. These regulations include a minimum disinfection of:

3 log (99.9%) for Giardia lamblia cysts
4 log (99.99%) for enteric viruses

In "water treatment terms" 1 log inactivation is referred to as 1 credit inactivation. Different types of filtration are assigned certain removal credits. For example, conventional filtration is worth 2.5 credits for Giardia cysts. Since the EPA requires 3 log (credit) removal, an additional 0.5 credit inactivation from disinfection must be attained.

Varying degrees of disinfection can be attained by altering the type and concentration of disinfectant, as well as the time water is in contact with the disinfectant. The decision to use one type of disinfectant versus another will set the precedence for the remainder of the values needed to attain the proper disinfection. The time untreated water is exposed to the disinfectant and the concentration of that disinfectant are the main factors in the equation that will be discussed in the next section. (Notice that the units of contact time are (mg/l)(min).)

History

A relationship between kill efficiency and contact time, was developed by Harriet Chick while she was a Fellow in the Pasteur institute in Paris, France. The research yielded data supporting her relationship that is shown in Figure 2 below. (No) represents the initial number of organisms and N is the number of organisms at time t. As contact time between water and disinfectant increases, the ratio of No/N decreases as Chick's Law predicts.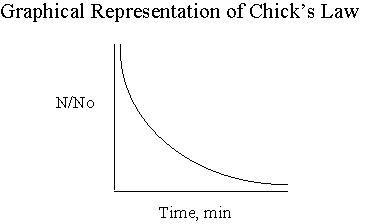

Figure 2 Taken from R.C. Hoehn’s CE 4104 Spring Notes

Watson later modified Chick's equation to account for varying types of disinfectants. He developed coefficients that better represented the strength of the disinfectant as well as the pH of the water. From this research, the coefficient of specific lethality (lambda) was developed. Watson’s modification of Chick’s equation is shown below.

Factors Affecting C*t Values

As pH increases the value of C*t also needs to be increased. This can be explained by examining the effects of pH on free chlorine. As the pH increases, more of the weak disinfectant (OCl-) exists than the strong disinfectant (HOCl-), thus increasing the C*t value. Refer to Table 1 below.

The greater log removal needed, the greater the C*t needs to be, as can be seen in Table 1.

Table 1: C*t for Removal of Giardia Cysts in Relation to Log Removal and pH

Log Removal	pH <6	pH 6.5	pH 7.0	pH 7.5
1.0	46	54	65	79
1.5	69	82	98	119
2.0	91	109	130	158
2.5	114	136	163	198

Information from the Virginia Department of Health Waterworks Regulations

The strength of a disinfectant directly affects the C*t. For a weak disinfectant, the C*t will have to be higher than for a strong disinfectant. As Table 2 below shows, ozone is the strongest disinfectant, thus the C*t value required is less when compared to chlorine and chlorine dioxide.

Different organisms have different resistances to disinfectants. If an organism has a strong resistance to a certain disinfectant, the C*t will be higher than for an organism with a weaker resistance. Refer to Table 2 below.

Table 2: C*t Values for the 99% Inactivation at 5 Degrees Celsius of Organisms Using Various Disinfectants

Organism	Free Chlorine (pH 6-7)	Chlorine Dioxide (pH 6-7)	Ozone (pH 6-7)
E.Coli	0.034-0.05	0.4-0.75	0.02
Rotavirus	0.01-0.05	0.2-2.1	0.006-0.06
Giardia lamblia cysts	47-150	-	0.5-0.6
Crytosporidium parvum	7200*	79*	5-10*

* 99% inactivation at 25 degrees C

Hoff, J.C., Inactivation of Microbial Agents by Chemical Disinfectants, EPA/600/2-86/067, 1986

Applications to Real Systems

Contact time and credit are essential in the design of a water treatment plant. In addition to the Environmental Protection Agency, the Virginia Department of Health regulates these values. Regulations governing credit have been discussed above, but contact time is dependent upon the specific plant. Most plants attain the required C*T in the clearwell, and the Blacksburg Water Authority (BAT) is no exception.

Since its creation in 1950, the water demand in the area has risen sharply. The BAT has been forced to convert all available space to expand the size of the c learwell. The result is a poorly baffled clearwell that does not retain the water long enough to get the credit it needs to meet regulations.

The following calculations are not entirely relevant to this topic, but the result is. They are taken from actual calculations by Jennifer Barber for the Blacksburg Water Authority in 1991. Before beginning the calculations, two terms must be defined. T-theo is the time one drop of water spends in the clearwell, theoretically. Baffling factor, BF, is a term that accounts for the mixing that occurs in the clearwell. Short-circuiting can be avoided by proper baffling. Below is a table of BF values.

Table 3: Baffling Factor Values

Baffling Condition	BF	Baffling Description
Unbaffled (Mixed Flow)	0.1	No baffling; very low length to width ratio
Poor	0.3	Single or multiple unbaffled inlets and outlets; no intrabasin baffles
Average	0.5	Baffled inlet or outlet with some intrabasin baffles
Superior	0.7	Perforated inlet baffle, serpentine, end-around, or perforated intrabasin baffles

Notes of Jerry Higgins (1991), Blacksburg Water Authority

The Blacksburg Water Authority attains credit for disinfection in the clearwell. The volume of the clearwell is 162,760 gallons, and the flow out of the clearwell is 12.4 MGD.

  T-theo = (162,760 gal) / [ 12.4 MGD*694.4 GPM/MGD ] = 18.9 min
  BF = 0.4 for BAT
  T10 = (0.4)(18.9min) = 7.56 min

At a pH = 7.8, chlorine residual = 1.0mg/l
  temperature = 1 degree Celsius
  log inactivation desired = 0.5   (to supplement the 2.5 credits from using sand filtration)
the required C*t = 45 (mg/l)(min)
BUT
with a T10 = 7.56, the C*t available at BAT = (7.56 min)(1 mg/l) = 7.56 (mg/l)(min)

This corresponds to a log inactivation available of 0.084. This is well below the desired credit of 0.5. The Blacksburg Water Authority is investigating possible solutions to this problem. Adjusting the pH with the use of caustic (as shown in Figure 4) could increase the effectiveness of the disinfectant. This would increase the concentration of (HOCl), which is more efficient and powerful than its counterpart, (OCl^-).

Figure 4: Blacksburg Water Authority Caustic Addition System

The most likely solution, though, will involve the construction of an on-site storage facility. This will increase the time water is in contact with the chlorine, thus increasing the log inactivation and credit for disinfection.

Credits and Links

We would like to thank those who made this project possible. Dr. Hoehn and Dr. Gallagher of Virginia Tech provided us with technical information and computer assistance. Jerry Higgins of the Blacksburg Water Authority took the time to show us how this topic applied to his water treatment plant. For more information regarding Blacksburg's water supply, visit their web site at
www.nrv.net/~h2o4u.

Water Treatment Table of Contents

Previous Topic

Next Topic